Гаага
Опубликовал рассказ о Гааге.
Позднее
Ctrl + ↑
Читателю предлагается несколько старых фотографий Челябинска
Вывод заголовка из блога на сайте
Вы, наверное, заметили, что у меня в меню на сайте справа от пункта «Блог» выводится заголовок последней заметки. Читатели спрашивают, как сделать так же на своём сайте с Эгеей. Я делаю очень тупо:
// читаем кеш главной страницы
$s = @file_get_contents ('meanwhile/user/caches/frontpage.ctree.psa');
$s = @unserialize ($s);
// берём тайтл первого элемента
$blog_aftertext = @$s[0]['title'];
if (!$blog_aftertext) {
// если не получилось, пробуем взять кеш главной страницы залогиненного пользователя
$s = @file_get_contents ('meanwhile/user/caches/frontpage-author.ctree.psa');
$s = @unserialize ($s);
// но тут надо быть осторожнее: в кеше могут быть скрытые заметки (собственно, поэтому
// кеш раздельный), поэтому находим тайтл ближайшей видимой и опубликованной заметки
$i = 0;
while (@$s[$i] and !($s[$i]['published?'] and $s[$i]['visible?'])) $i ++;
if ($s[$i]['published?'] and $s[$i]['visible?']) {
$blog_aftertext = $s[$i]['title'];
}
}Если ни там, ни сям не нашлось (например, кеш ещё не успел собраться), то и фиг с ним.
Естественно, никто не обещает, что в следующей версии Эгеи кеш будет устроен так же, поэтому это не очень промышленное решение. Но меня вполне устраивает. Может, и вам подойдёт.
На днях я рассказывал, как хреново работает Фейсбук с длинными постами: обрезает в случайном месте, теряет место чтения при разворачивании
Сборка Эгеи 2725
Короче, дед Мороз принёс вам новую сборку Эгеи — 2725. Это что-то вроде бета-версии релиза 2.3, который скоро будет зарелизен.
Ура:
＊ УТФ-8 ＊
Помните заметку про числа π и e? Число π там написано нормальной греческой буквой π, и ничего не взрывается.
Главная благодарность в этой связи Жене Степанищеву за его серию статей о переходе на УТФ-8. Если вы будете обновлять со старой версии, обязательно-обязательно сделайте бекап. Движок попытается сконвертировать все существующие данные в УТФ-8. Естественно, если вы делали свои темы оформления или допблоки, это всё надо будет тоже сконвертировать в УТФ-8. Пользуясь случаем, благодарю ещё и Игоря Васильковского, который писал бекап, за то, что он работает с УТФ-8 без вопросов.
Из других новостей:
- теперь есть интерфейс выбора урла заметки;
- у черновиков тоже теперь текстовые урлы, а не идентификаторы — сразу видно, какой будет урл, когда опубликуется;
- если сохранить заметку или черновик с новым урлом по ⌘S, адрес мгновенно поменяется прямо адресной строке (если у вас хороший браузер);
- выбор времени публикации заметки теперь живёт прямо в редакторе (больше нет монструозного экрана на эту тему);
- выбор языка интерфейса в настройке (в комплекте идут русский и английский, если вы хотите сделать свой перевод на другой язык, сначала свяжитесь со мной);
- больше нет дурацких собак в админских урлах (кроме адских системных урлов вроде /@sync);
- существенная оптимизация всего-всего;
- исправлен баг, из-за которого при перетаскивании в текст заметки нескольких картинок, вставлялась только одна;
- что-то там подкрутили с Артёмом Поликарповым в интеграции Фоторамы;
- что-то там улучшили с Муратом Шидаковым в интерфейсе ввода тегов;
- тоненькие подчёркивания ссылок!
Пока нет документации по обновлению шаблонов и всего такого. Всё на свой страх и риск. Если вы не любите экспериментировать, лучше пока не обновляться. И не забывайте, что техподдержки нет.
Чтобы обновиться, нужно заменить .htaccess, папку /system/ и все подпапки /themes/ новыми, а вот и ссылка на архив.
С новым счастьем!
Заимствования
Несколько коротких фрагментов.
Иоганнес Брамс. Симфония № 3. I:
Густав Малер. Симфония № 6. I:
• • • • •
Александр Бородин. Половецкие пляски из оперы «Князь Игорь». Пляска девушек плавная:
Сергей Рахманинов. Симфонические танцы. I:
• • • • •
Пётр Чайковский. «Лебединое озеро». Действие второе. Сцена. По озеру плывёт стая белых лебедей:
Дмитрий Шостакович. Симфония № 7 «Ленинградская». II:
Вчера я завёл себе профиль на Промодиджее, а сегодня закачал туда небольшой промо-микс
В 2007 году я выпустил трек «Линкс» (прогрессив-хаус). У меня новая версия, с чуточку подтянутым звуком
Что почитать на выходных — 39
Вот что:
- Антарктида и Южный полюс. Артемий Лебедев рассказывает о поездке. Крутота.
- Формула Эйлера и приближенные методы. Роман Парпалак наглядно объясняет, почему же
eiπ = −1. Заодно из его заметки становится понятно, почему же e определяется именно как предел y = (1 + 1 / x)x при x → ∞. - История авторского права в семи частях. Смысл в том, что во все времена защитники авторских прав реально боролись лишь за права посредников, но не авторов и не потребителей.
- Everything is my fault. Крутая мировоззренческая концепция.
- Page Weight Matters. Почему важно, чтобы страницы весили поменьше.
Как-то раз был в Берлине в баре с двумя красивыми девушками. Более того, речь пойдёт о том, что происходило в туалете
Восьмая версия сайта
Я открыл восьмую версию сайта.
Наконец-то у сайта появилось внятное меню, и блог стал одним из его пунктов. Теперь из блога не страшно перейти, скажем, в «Проекты» — всегда можно вернуться назад. Да, дизайн самого блога, соответственно, стал совсем другим.
Новая главная страница стала красивее и веселее (а ещё она прикольно тянется).
На всех страницах, доступных на двух языках, теперь есть переключалка в правом верхнем углу. Вообще, английская версия сайта стала чуть более полноценной.
Раздел «Музыка» стал клёвым! Я навёл порядок в музыке, оформил странички двух своих альбомов, и теперь всё можно слушать прямо на сайте. Миксы попали под нож ФФФа, появятся когда-нибудь потом.
Полагаю, ещё несколько дней будет турбулентность (всё время всплывают какие-то баги), но в целом уже всё похоже на правду.
Как я и предполагал, ко мне на сайт заходят клёвые люди, которые занимаются интересными вещами. Пусть про это узнает чуть большая аудитория
Личное присутствие
Пара цитат. Раз:
Когда знаешь, что надо делать, личное присутствие — это всего лишь дань традиции, но не показатель эффективности.
Артемий Лебедев. Тяга к перемене мест
Два:
Минимальные системные требования: необходимость приходить в студию каждый рабочий день (удаленной работы у нас нет)...
Из раздела «Вакансии» на сайте Студии Лебедева
Нет ли здесь противоречия? См. также Комьют.
Числа π и e
Все знают геометрический смысл числа π — это длина окружности с единичным диаметром:
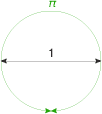
А вот смысл другой важной константы, e, имеет свойство быстро забываться. То есть, не знаю, как вам, а мне каждый раз стоит усилий вспомнить, чем же так замечательно это число, равное 2,7182818284590... (значение я, однако, по памяти записал). Поэтому я решил написать заметку, чтобы больше из памяти не вылетало.
Число e по определению — предел функции y = (1 + 1 / x)x при x → ∞:
| x | y | |
| 1 | (1 + 1 / 1)1 | = 2 |
| 2 | (1 + 1 / 2)2 | = 2,25 |
| 3 | (1 + 1 / 3)3 | = 2,3703703702... |
| 10 | (1 + 1 / 10)10 | = 2,5937424601... |
| 100 | (1 + 1 / 100)100 | = 2,7048138294... |
| 1000 | (1 + 1 / 1000)1000 | = 2,7169239322... |
| ∞ | lim× → ∞ | = 2,7182818284590... |
Это определение, к сожалению, не наглядно. Непонятно, чем замечателен этот предел (несмотря на то, что он называется «вторым замечательным»). Подумаешь, взяли какую-то неуклюжую функцию, посчитали предел. У другой функции другой будет.
Но число e почему-то всплывает в целой куче самых разных ситуаций в математике.
Для меня главный смысл числа e раскрывается в поведении другой, куда более интересной функции, y = kx. Эта функция обладает уникальным свойством при k = e, которое можно показать графически так:
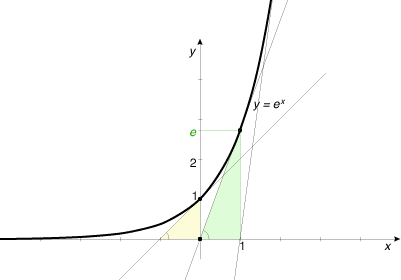
В точке 0 функция принимает значение e0 = 1. Если провести касательную в точке x = 0, то она пройдёт к оси абсцисс под углом с тангенсом 1 (в жёлтом треугольнике отношение противолежащего катета 1 к прилежащему 1 равно 1). В точке 1 функция принимает значение e1 = e. Если провести касательную в точке x = 1, то она пройдёт под углом с тангенсом e (в зелёном треугольнике отношение противолежащего катета e к прилежащему 1 равно e). В точке 2 значение e2 функции снова совпадает с тангенсом угла наклона касательной к ней. Из-за этого, заодно, сами касательные пересекают ось абсцисс ровно в точках −1, 0, 1, 2 и т. д.
Среди всех функций y = kx (например, 2x, 10x, πx и т. д.), функция ex — единственная обладает такой красотой, что тангенс угла её наклона в каждой её точке совпадает со значением самой функции. Значит по определению значение этой функции в каждой точке совпадает со значением её производной в этой точке: (ex)´ = ex. Почему-то именно число e = 2,7182818284590... нужно возводить в разные степени, чтобы получилась такая картинка.
Именно в этом, на мой вкус, состоит его смысл.
Числа π и e входят в мою любимую формулу — формулу Эйлера, которая связывает 5 самых главных констант — ноль, единицу, мнимую единицу i и, собственно, числа π и е:
eiπ + 1 = 0
Почему число 2,7182818284590... в комплексной степени 3,1415926535...i вдруг равно минус единице? Ответ на этот вопрос выходит за рамки заметки и мог бы составить содержание небольшой книги, которая потребует некоторого начального понимания тригонометрии, пределов и рядов.
Меня всегда поражала красота этой формулы. Возможно, в математике есть и более удивительные факты, но для моего уровня (тройка в физико-математическом лицее и пятёрка за комплексный анализ в универе) это самое главное чудо.
Update (17.06.2005): Правильный ответ
Кредитные карты
Тёма сегодня спрашивает, уходите ли вы в минус по кредитке. Я даже удивился такой постановке вопроса: ясное дело, что уходим, нафига иначе эта кредитка вообще? Потом подумал, что, наверное, кто-то и не уходит, ведь со словом «кредит» связано много страха и недопонимания.
Кредит многими воспринимается только как способ взять в долг, когда своих денег нет. Влезать в долги не очень приятно, а уход в минус по кредитке — это вроде как оно и есть. Ещё многие думают, что кредит — это когда банк тебя обдирает, даёт деньги и незаметно заставляет вернуть намного больше (в народе придуман даже смешной термин «переплата» — ну, про это в другой раз).
На самом деле уходить в минус по кредитке следует вовсе не потому, что нет своих денег, а потому что это выгодно. Когда я это понял, тогда я и завёл кредитку — до этого у меня была обычная дебетовая карта.
Дело в том, что деньги стоят денег. Поэтому имеет смысл тратить те, которые дешевле. Особенно приятно тратить бесплатные деньги. Зачем использовать свои, которые выгодно где-то лежат, когда можно бесплатно использовать банковские? В «Альфа-банке», например, 100 дней беспроцентного погашения задолженности дают, а «Связной банк», тем временем, ежемесячно начисляет аж 10% годовых на остаток. Совершенно естественно со сладкой улыбкой наблюдать за тем, как тебе капают связные проценты, на халяву тратя альфовские рубли.
При покупке кефира разницы особой нет, но если надо съездить в отпуск, а там взять машину напрокат, то разницу уже видно, и она многократно покрывает стоимость обслуживания кредитки.
Видео по вторникам: Нидерланды
Чувак, который когда-то сделал гениальное видео про разницу между Великобританией и Соединённым Королевством, продолжает тему. На этот раз — про Голландию и Нидерланды. Всё не так просто, как кажется:
У него ещё есть крутое видео про «Лондон» и The City of London в двух частях — раз, два. Особенно смешной рассказ во второй части про то, как стать мэром Сити.
Да, ну и про Плутон тоже посмотрите, конечно.
Ранее
Ctrl + ↓