Саммит большой восьмёрки
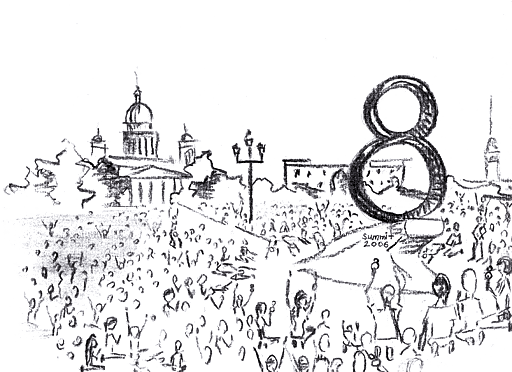
Идея моя, иллюстрация — Саши Лукьянович.
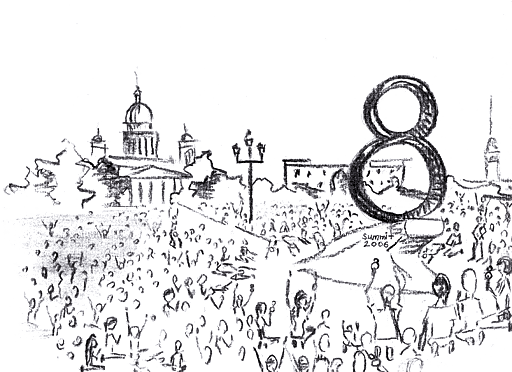
Идея моя, иллюстрация — Саши Лукьянович.
К сожалению, некоторые люди считают, что если они знают теорию рядов, то значит без неё никаких метаматических понятий вводить нельзя. Более того, эти люди полагают, что тот, кто не использует её повсеместно, — невежда. Оставим воззрения этих людей на их совести. Давайте лучше разберёмся с тем, что такое бесконечная периодическая дробь и как с ней быть нам, необразованным людям, не знающим пределов.
Поделим 237 на 5. Нет, не нужно запускать «Калькулятор». Давайте лучше вспомним среднюю (или даже начальную?) школу и просто поделим столбиком:
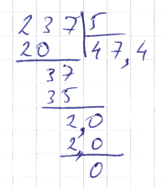
Ну как, вспомнили? Тогда можно и к делу переходить.
Понятие «дробь» в математике имеет два значения:
Существует два вида дробей — в смысле, две формы записи нецелых чисел:
Заметим, что вообще само использование дроби-записи не означает, что записанное есть дробь-число, например 3/3 или 7,0 — не дроби в первом смысле слова, но во втором, конечно, дроби.
В математике, вообще искони принят счёт десятичный, а потому и десятичные дроби удобнее простых, т. е. дробь с десятичным знаменателем (Владимир Даль. Толковый словарь живого великорусского языка. «Десять»).
А раз так, то хочется всякую дробь вертикальную сделать десятичной («горизонтальной»). А для этого нужно просто-напросто числитель поделить на знаменатель. Возьмём, например, дробь 1/3 и попробуем сделать из неё десятичную.
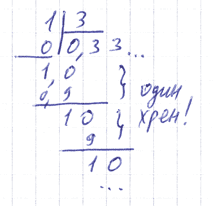
Даже совсем необразованный заметит: сколько ни дели — не разделится: так и будут тройки до бесконечности появляться. Так и запишем: 0,33... Имеем в виду при этом «число, которое получается, когда делишь 1 на 3», или, короче, «одна третья». Естественно, что одна третья — дробь в первом смысле слова, а «1/3» и «0,33...» — дроби во втором смысле слова, то есть формы записи числа, которое находится на числовой прямой на таком расстоянии от нуля, что если трижды его отложить, получится единица.
Теперь попробуем разделить 5 на 6:
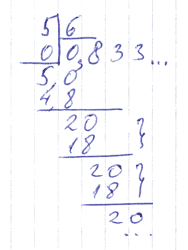
Снова запишем: 0,833... Имеем в виду «число, которое получается, когда делишь 5 на 6», или, короче, «пять шестых». Однако, тут возникает путаница: имеется ли в виду 0,83333 (и дальше тройки повторяются), или же 0,833833 (и дальше 833 повторяется). Поэтому запись с многоточием нас не устраивает: непонятно, откуда начинается повтряющаяся часть (она называется «период»). Поэтому период мы будем брать в скобки, вот так: 0,(3); 0,8(3).
0,(3) не просто равно одной третьей, это есть одна третья, ведь мы специально эту запись придумали, чтобы представлять это число в виде десятичной дроби.
Эта запись и называется бесконечной периодической дробью, или просто периодической дробью.
Всегда, когда мы делим одно число на другое, если не получается дробь конечная, то получается дробь бесконечная периодическая, то есть обязательно когда-нибудь последовательности цифр начнут повторяться. Почему это так можно понять чисто умозрительно, посмотрев внимательно на алгоритм деления столбиком:
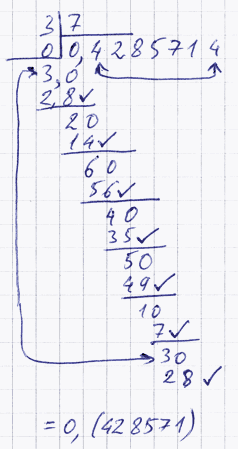
В местах, обозначенных галочками, не могут всё время получаться разные пары чисел (потому, что таких пар в принципе конечное множество). А как только там появится такая пара, которая уже была, разность тоже будет такой же — и дальше весь процесс начнёт повторяться. Нет нужды проверять это, ведь совершенно очевидно, что при повторении тех же действий результаты будут те же.
Теперь, когда мы хорошо понимаем суть периодической дроби, давайте попробуем умножить одну треть на три. Да, получится, конечно, один, но давайте запишем эту дробь в десятичной форме и умножим столбиком (двусмыслицы из-за многоточия здесь не возникает, так как все цифры после запятой одинаковые):
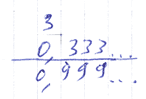
И снова мы замечаем, что всё время будут после запятой появляться девятки, девятки и девятки. То есть, используя, обратно, скобочную запись, мы получим 0,(9). Поскольку мы знаем, что произведение одной трети и трёх есть единица, то 0,(9) — это такая вот причудливая форма записи единицы. Однако использовать такую форму записи нецелесообразно, ведь единица прекрасно записывается и без использования периода, вот так: 1.
Как видим, 0,(9) — это один из тех случаев, когда целое число записано в форме дроби, вроде 3/3 или 7,0. То есть, 0,(9) — это дробь лишь во втором смысле слова, но никак не в первом.
Вот так, безо всяких пределов и рядов мы разобрались с тем, что такое 0,(9) и как с ним бороться.
Но всё же вспомним о том, что на самом-то деле мы умные и изучали анализ. Действительно, трудно отрицать, что:
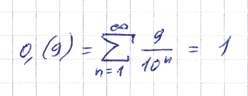
Но, пожалуй, никто не будет спорить и с тем, что:
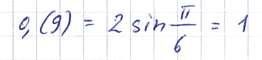
Или:

Всё это, конечно, верно. Действительно, 0,(9) является и суммой приведённого ряда, и удвоенным синусом указанного угла, и натуральным логарифмом числа Эйлера.
Но ни то, ни другое, ни третье не является определением.
Утверждать, что 0,(9) — сумма бесконечного ряда 9/(10n), при n от единицы, — это всё равно, что утверждать, что синус — это сумма бесконечного ряда Тейлора:
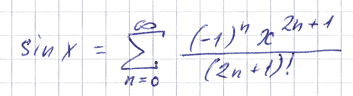
Это совершенно верно, и это является важнейшим фактом для вычислительной математики, но это не определение, и, что самое главное, это ничуть не приближает человека к пониманию сути синуса. Суть же синуса некоторого угла состоит в том, что это всего навсего отношение противолежащего углу катета к гипотенузе.
Дак вот, периодическая дробь — это всего навсего десятичная дробь, которая получается, когда при делении столбиком один и тот же набор цифр повторется. Анализа тут нет и в помине.
И вот тут-то возникает вопрос: откуда вообще мы взяли число 0,(9)? Что на что мы делим столбиком, чтобы его получить? Действительно, нет таких чисел, при делении которых друг на друга столбиком мы бы имели бесконечно появляющиеся девятки. Но нам же удалось получить это число, умножая столбиком 0,(3) на 3? Не совсем. Ведь умножать нужно справа налево, чтобы корректно учитывать переносы разрядов, а мы это делали слева направо, хитро воспользовавшись тем, что переносов нигде всё равно не возникает. Поэтому правомерность записи 0,(9) зависит от того, признаём ли мы правомерность такого умножения столбиком или нет.
Следовательно, можно вообще сказать, что запись 0,(9) некорректна — и в определённой степени быть правым. Однако, поскольку нотация a,(b) принята, то просто некрасиво отказываться от неё при b = 9; лучше определиться с тем, что такая запись означает. Так что, если мы вообще принимаем запись 0,(9), то эта запись, конечно, означает число один.
Осталось лишь добавить, что если бы мы использовали, скажем, троичную систему счисления, то при делении столбиком единицы (13) на тройку (103) получилось бы 0,13 (читается «ноль целых одна третья»), а при делении единицы на двойку получилось бы 0,(1)3.
Так что периодичность дроби-записи — это не объективная какая-то характеристика дроби-числа, а всего лишь побочный эффект использования той или иной системы счисления.
Сегодня моему сайту исполняется 5 лет, и связи с этим я, наконец-то, запустил новую, шестую его версию.
На сайте открылся новый большой раздел Bild с кучей разных фотографий, которые разделены по категориям, например:
Также несколько разделов вышли из подполья:
В полностью переработанное Портфолио добавлены работы, сделанные за последние полгода-год, которых раньше было нигде не найти:
Туда же добавлены хорошие, но не принятые работы:
И ещё там теперь можно посмотреть историю версий этого сайта.
Ну и, наконец, новости сайта стали доступны в RSS.
Пожалуйста, походите по сайту и скажите, что и где у меня глючит в каком браузере.
Удивительно, что люди не понимают, что 0,(9) = 1, и знак равенства здесь используется в буквальном смысле.
Вчера Дмитрий Кирсанов прислал мне ссылку на подробное объяснение того, почему 0,(9) = 1 (на английском языке; автор развивает тему также в нескольких последующих заметках).
Развлекло меня в этой статье в первую очередь то, что когда я объяснял этот факт одному человеку где-то полгода назад, я использовал все те же самые доводы, причём в том же порядке. Ещё недавно я оставлял на эту тему комментарий у Реймонда Чена.
Насколько я вижу проблему, многие люди просто концептуально не понимают, как что-то может не стремиться, а «быть равным» бесконечности. Они говорят, что «0,(9) стремится, но не равно 1».
Но 0,(9) — это не последовательность и не функция, а число. Число не может никуда стремиться, оно стоит себе на месте на числовой прямой и не дёргается.
Действительно, последовательность 0,9; 0,99; 0,999; и т. д., при стремлении количества девяток к бесконечности, будет стремиться к единице. Но когда девяток станет ровно бесконечное количество — а именно это выражает запись 0,(9), — тогда это число станет ровно единицей.
Запись 0,(9) означает не то, что девяток в числе становится «всё больше и больше», а то, что их есть бесконечное количество прямо сейчас.
Естественно, что это то же самое число, что и 1.
Update: Продолжение темы.
«Может быть, дойдет и до роботов. Но без участия человека это невозможно. Главное — это пограничник», — сказал глава государства.
(См. стенограмму)
Тем временем «Большую информационную программу „Эхо“» на «Эхе Москвы» завершили приблизительно так (цитирую по памяти):
Некоторые популярные вопросы остались без ответа, в частности, россияне так и не узнают об отношении президента к популярному персонажу интернет-шуток — медведу.
В прошлом выпуске новостей на «Серебряном дожде» Николай Пивненко огласил список самых популярных вопросов президенту. Как вы, вероятно, знаете, вопросы это — следующие:
Перед тем, как прочитать второй вопрос, Николай оговорился, что нормальные люди, не знакомые со спецификой жизни в интернете, не поймут, откуда он такой взялся.
Ссылку опубликовал сегодня Джоуэл Сполски, опубликую её и я.
Некто Ник Гравгард предложил новую интерпретацию символа табуляции, которая позволит отказаться от моноширинных шрифтов в пользу пропорциональных, несколько облегчить форматирование кода и сделать его в некоторых случаях более опрятным.
Не знаю, насколько удобно будет этим пользоваться, но идея в любом случае симпатичная.
Правда, на мой взгляд, моноширинные шрифты всё равно предпочтительнее для кода. В частности, разбираться в длинных выражениях с множеством скобок лучше именно с ними.
Лебедев переименовал 133-й параграф из «Знака паузы» в «Двоезапятие» (да, хорошее слово) и в значительной степени переписал его текст. В новом виде всё это по-прежнему создаёт впечатление дурацкой идеи, однако теперь она подаётся как бы чуточку аккуратнее.
Автору известна судьба типографических нововведений — редкие из них наслаждаются популярностью. Но [...] двоезапятие может оказаться востребованным и актуальным в современных текстах.
Забавно, что со стороны читателя, который видел и первую версию, это выглядит так, будто Лебедев вступает с ним в диалог:
Чёрт его знает, конечно, но мне так кажется, что когда-нибудь после 132-го параграфа в Ководстве будет идти 134-й.
Раньше звонок с городского на мобильник оплачивался владельцем мобильника*, поэтому был не очень приличным делом. С 1 июля за все звонки платит звонящий, и поэтому теперь можно без зазрения совести звонить на мобильный с городского (например, при моём тарифном плане это получается значительно дешевле).
Но есть несколько нюансов.
Во-первых, про это ещё не все знают. Не будешь же при каждом звонке объяснять, что «это для вас бесплатно». Поэтому про тебя будут думать плохо. Но это явление временное.
Во-вторых, городских номеров чаще всего ни у кого в мобильнике не записано, и поэтому люди не будут понимать, кто им звонит. А это как бы тоже не очень красиво.
И, в-третьих, городские номера у большинства людей не являются личными, поэтому даже если городской номер записан на конкретного человека, это ещё не гарантирует того, что звонит именно этот человек. Так что тоже создаётся некое «ощущение дискомфорта».
Поэтому ещё десять раз подумаешь, перед тем, как позвонить с городского.
* За исключением редких тарифных планов, в которых бесплатность всех входящих была «фишкой»
Если зайти на сайт вопросов президенту, и открыть страницу актуальных тем, то многое станет ясно о политической ситуации в стране и о взгляде общества на неё.
Личные вопросы президенту занимают одно из первых мест в «облаке» тем. Слов вроде «демократия», «свобода слова», «права человека» там нет вообще (действительно, кого это интересует), а в теме «Ходорковский» большая часть вопросов распадается на категории «почему дали так мало» и «когда посадят остальных олигархов».
Главное же, что волнует россиян, — почему Путин поцеловал мальчика в живот и когда в стране легализуют марихуану.