Бесконечные периодические дроби

К сожалению, некоторые люди считают, что если они знают теорию рядов, то значит без неё никаких метаматических понятий вводить нельзя. Более того, эти люди полагают, что тот, кто не использует её повсеместно, — невежда. Оставим воззрения этих людей на их совести. Давайте лучше разберёмся с тем, что такое бесконечная периодическая дробь и как с ней быть нам, необразованным людям, не знающим пределов.

Поделим 237 на 5. Нет, не нужно запускать «Калькулятор». Давайте лучше вспомним среднюю (или даже начальную?) школу и просто поделим столбиком:

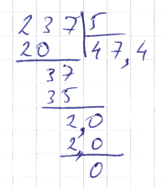
Ну как, вспомнили? Тогда можно и к делу переходить.

Понятие «дробь» в математике имеет два значения:

1. Нецелое число.
2. Форма записи нецелого числа.

Существует два вида дробей — в смысле, две формы записи нецелых чисел:

1. Простые (или вертикальные) дроби, вроде 1/2 или 237/5.
2. Десятичные дроби, например, 0,5 или 47,4.

Заметим, что вообще само использование дроби-записи не означает, что записанное есть дробь-число, например 3/3 или 7,0 — не дроби в первом смысле слова, но во втором, конечно, дроби.

В математике, вообще искони принят счёт десятичный, а потому и десятичные дроби удобнее простых, т. е. дробь с десятичным знаменателем (Владимир Даль. Толковый словарь живого великорусского языка. «Десять»).

А раз так, то хочется всякую дробь вертикальную сделать десятичной («горизонтальной»). А для этого нужно просто-напросто числитель поделить на знаменатель. Возьмём, например, дробь 1/3 и попробуем сделать из неё десятичную.

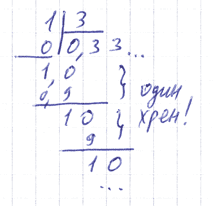
Даже совсем необразованный заметит: сколько ни дели — не разделится: так и будут тройки до бесконечности появляться. Так и запишем: 0,33... Имеем в виду при этом «число, которое получается, когда делишь 1 на 3», или, короче, «одна третья». Естественно, что одна третья — дробь в первом смысле слова, а «1/3» и «0,33...» — дроби во втором смысле слова, то есть формы записи числа, которое находится на числовой прямой на таком расстоянии от нуля, что если трижды его отложить, получится единица.

Теперь попробуем разделить 5 на 6:

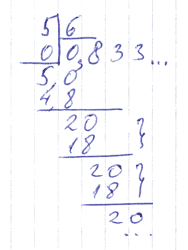
Снова запишем: 0,833... Имеем в виду «число, которое получается, когда делишь 5 на 6», или, короче, «пять шестых». Однако, тут возникает путаница: имеется ли в виду 0,83333 (и дальше тройки повторяются), или же 0,833833 (и дальше 833 повторяется). Поэтому запись с многоточием нас не устраивает: непонятно, откуда начинается повтряющаяся часть (она называется «период»). Поэтому период мы будем брать в скобки, вот так: 0,(3); 0,8(3).

0,(3) не просто равно одной третьей, это есть одна третья, ведь мы специально эту запись придумали, чтобы представлять это число в виде десятичной дроби.

Эта запись и называется бесконечной периодической дробью, или просто периодической дробью.

Всегда, когда мы делим одно число на другое, если не получается дробь конечная, то получается дробь бесконечная периодическая, то есть обязательно когда-нибудь последовательности цифр начнут повторяться. Почему это так можно понять чисто умозрительно, посмотрев внимательно на алгоритм деления столбиком:

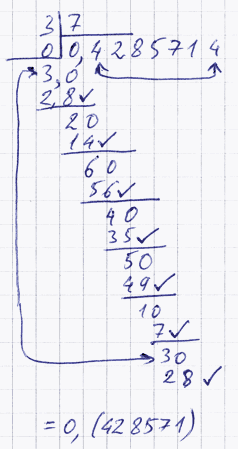
В местах, обозначенных галочками, не могут всё время получаться разные пары чисел (потому, что таких пар в принципе конечное множество). А как только там появится такая пара, которая уже была, разность тоже будет такой же — и дальше весь процесс начнёт повторяться. Нет нужды проверять это, ведь совершенно очевидно, что при повторении тех же действий результаты будут те же.

Теперь, когда мы хорошо понимаем суть периодической дроби, давайте попробуем умножить одну треть на три. Да, получится, конечно, один, но давайте запишем эту дробь в десятичной форме и умножим столбиком (двусмыслицы из-за многоточия здесь не возникает, так как все цифры после запятой одинаковые):

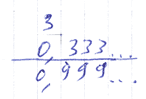
И снова мы замечаем, что всё время будут после запятой появляться девятки, девятки и девятки. То есть, используя, обратно, скобочную запись, мы получим 0,(9). Поскольку мы знаем, что произведение одной трети и трёх есть единица, то 0,(9) — это такая вот причудливая форма записи единицы. Однако использовать такую форму записи нецелесообразно, ведь единица прекрасно записывается и без использования периода, вот так: 1.

Как видим, 0,(9) — это один из тех случаев, когда целое число записано в форме дроби, вроде 3/3 или 7,0. То есть, 0,(9) — это дробь лишь во втором смысле слова, но никак не в первом.

Вот так, безо всяких пределов и рядов мы разобрались с тем, что такое 0,(9) и как с ним бороться.

Но всё же вспомним о том, что на самом-то деле мы умные и изучали анализ. Действительно, трудно отрицать, что:

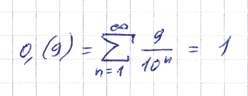
Но, пожалуй, никто не будет спорить и с тем, что:

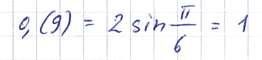
Или:

Всё это, конечно, верно. Действительно, 0,(9) является и суммой приведённого ряда, и удвоенным синусом указанного угла, и натуральным логарифмом числа Эйлера.

Но ни то, ни другое, ни третье не является определением.

Утверждать, что 0,(9) — сумма бесконечного ряда 9/(10ⁿ), при n от единицы, — это всё равно, что утверждать, что синус — это сумма бесконечного ряда Тейлора:

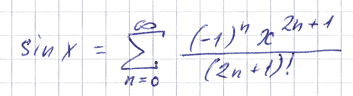
Это совершенно верно, и это является важнейшим фактом для вычислительной математики, но это не определение, и, что самое главное, это ничуть не приближает человека к пониманию сути синуса. Суть же синуса некоторого угла состоит в том, что это всего навсего отношение противолежащего углу катета к гипотенузе.

Дак вот, периодическая дробь — это всего навсего десятичная дробь, которая получается, когда при делении столбиком один и тот же набор цифр повторется. Анализа тут нет и в помине.

И вот тут-то возникает вопрос: откуда вообще мы взяли число 0,(9)? Что на что мы делим столбиком, чтобы его получить? Действительно, нет таких чисел, при делении которых друг на друга столбиком мы бы имели бесконечно появляющиеся девятки. Но нам же удалось получить это число, умножая столбиком 0,(3) на 3? Не совсем. Ведь умножать нужно справа налево, чтобы корректно учитывать переносы разрядов, а мы это делали слева направо, хитро воспользовавшись тем, что переносов нигде всё равно не возникает. Поэтому правомерность записи 0,(9) зависит от того, признаём ли мы правомерность такого умножения столбиком или нет.

Следовательно, можно вообще сказать, что запись 0,(9) некорректна — и в определённой степени быть правым. Однако, поскольку нотация a,(b) принята, то просто некрасиво отказываться от неё при b = 9; лучше определиться с тем, что такая запись означает. Так что, если мы вообще принимаем запись 0,(9), то эта запись, конечно, означает число один.

Осталось лишь добавить, что если бы мы использовали, скажем, троичную систему счисления, то при делении столбиком единицы (1₃) на тройку (10₃) получилось бы 0,1₃ (читается «ноль целых одна третья»), а при делении единицы на двойку получилось бы 0,(1)₃.

Так что периодичность дроби-записи — это не объективная какая-то характеристика дроби-числа, а всего лишь побочный эффект использования той или иной системы счисления.