Прямая линия из Индии в США и сумма углов треугольника
Как-то мне попалась такая картинка:
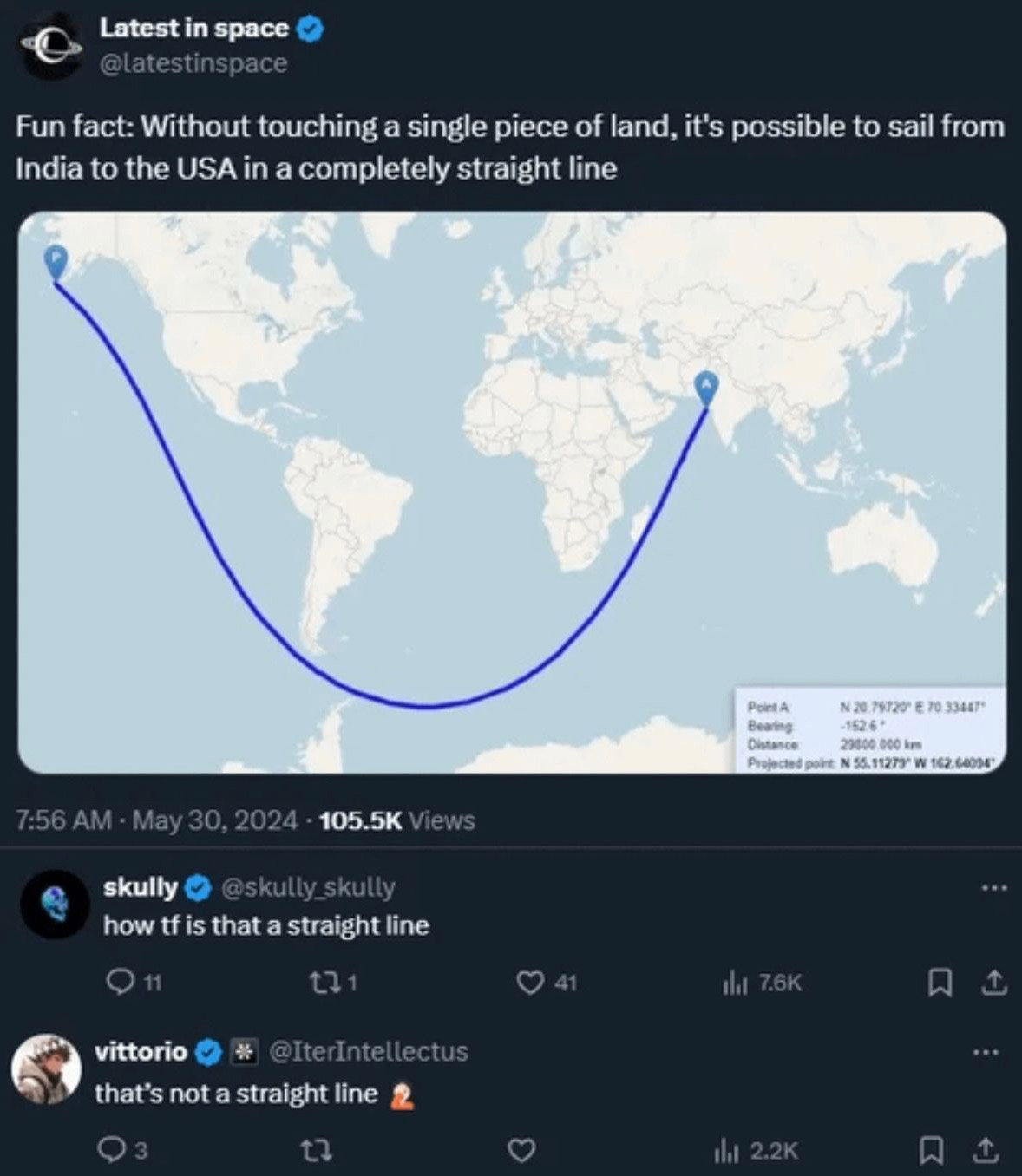
Автор твита утверждает, что можно добраться из Индии в США не касаясь суши по «полностью прямой линии». И мы видим комментарии, мол, с херов ли это прямая линия? Я присоединяюсь с комментариям: с херов ли это прямая линия?
Очевидно, картинка призвана выставить дурачкам комментаторов, которые не понимают, что Земля круглая, проекция всё искажает, но в настоящей жизни эта линия реально прямая. Да вот только это не так! Эта линия не прямая ровно именно потому, что Земля круглая! Эта линия загибается, потому что вся поверхность земли загибается!
Причём достаточно было бы переформулировать, сказав что-то вроде «не меняя курса» или даже «в строго прямом направлении», и всё было бы чётко. Но тут сказано даже не просто straight line, а прям completely straight line, как будто она вообще безоговорочно прямая.
Это мне напоминает мою фрустрацию в момент, когда в школе однажды говорят, мол, сумму углов треугольника может быть и не 180°. Нет, не может. Если мы рисуем треугольник на шаре, то это уже не треугольник, это другая фигура. Понятно, что в неевклидовой аксиоматике эту другую фигуру может быть очень естественно назвать треугольником, но в любом случае слово треугольник с этого мгновения значит не то, что значило только что. Другая фигура может обладать другими свойствами углов, и если «фокус» тут в том, что мы её назвали тем же словом, то это не очень сложный фокус, я его сразу раскусил.


Так она и есть полностью прямая. Но относительно поверхности шара, а не трехмерного пространства. Представь, что ты был бы двухмерным существом, живущим на этой поверхности. Мне кажется, без всяких вариантов ты бы назвал эту линию прямой
Самое важно слово в вашем комментарии — «но». То есть всё-таки не полностью.
Кстати, каким определением ты пользовался, чтобы сказать, что эта линия непрямая? А в математике у прямой вообще определения нет, она просто должна определенным аксиомам соответствовать
What you are saying is — «sailing in a straight line» is impossible to do at all. Real Petersonian nadmozg statement.
But the counterargument is — «sailing in a straight line» does not equal «sailing» + «geometric straight line», it’s a different thing that uses same words.
Если кто-то при взгляде на эту картинку чувствует себя дурачком, то это проблема только его образования. Картинка никого не пытается выставить дурачком, она показывает обычный fun fact, любопытный для тех, кто его не знает. Примерно как то, что Гренландия — часть Дании, самый западный регион России — Чукотка, а самый восточный штат США — Аляска.
Без контекста в школе никогда так не говорят, всегда сообщают, что это в других геометриях.
Буквоеды называют такую линию «геодезической». Но поскольку это «обобщение понятия „прямая“ для искривлённых пространств» («generalization of the notion of a „straight line“», раз уж исходное утверждение на английском), то имеет место всего лишь дополнительный уровень абстракции — в реальности-то даже настоящих прямых не существует. (Да и самого евклидова пространства — тоже, потому что пространство-время даже локально псевдоевклидово, а в человеческих масштабах ещё и сильно искривлено у поверхности Земли.)
Странно, что вы к слову «sail» не придрались, а то ведь _идти под парусом_ по любой заранее заданной траектории хрен получится...
В топологии это называется геодезическая линия — кривая, которая в искривлённых пространствах является «прямой».
https://ru.wikipedia.org/wiki/Геодезическая
Тут много к чему можно придраться. И к прямой в первую очередь. Геодезическую линию уже назвали, но есть и другие термины. Автор исходника имеет в виду ортодромию — линию на поверхности Земли, соединяющую две заданные точки и имеющую наименьшую возможную длину. Именно в этом смысле она «прямая». Я сам люблю точность в терминах, но придираться к ним в категории fun fact, кажется, все-таки не стоит.
А вот к «не меняя курса» у меня есть вопросы. Получающаяся при этом кривая — локсодромия — или в частном случае совпадает с параллелью, или, с позволения сказать неточно, «собирается в спираль» к одному из полюсов. Поэтому прокладка маршрута с постоянным курсом имеет смысл только на небольших дистанциях и в умеренных широтах.
К способу перемещения вопросов, впрочем, больше :). Если включить режим зануды, то можно сказать, что построить такой маршрут по «прямой» (ортодромии) можно, и даже не слишком сложно. А вот пройти его под парусами (to sail) будет, скорее всего, impossible. И даже на моторном судне задача окажется не очень простой, хотя и, скорее всего, решаемой.