Телеграм за неделю 8—14 января 2018
Вот как выглядела предыдущая неделя в моём канале в телеграме:
Понедельник, 8 января

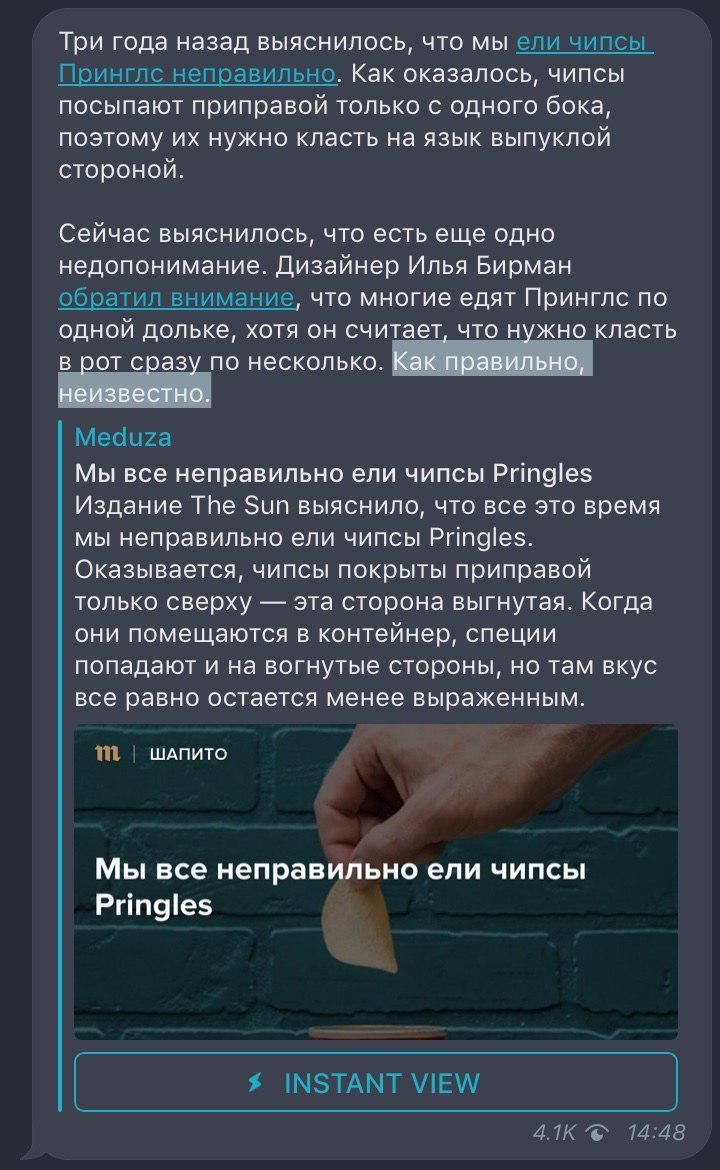

Рубрика «Отвечу голосом»: чем отличается проектирование схемы метро и схемы наземного транспорта?
Вторник, 9 января
Я всегда рекомендую ставить подписи слева от полей форм. А исследование Гугля якобы показывает, что лучше над полями.
Написал совет по этому поводу:
https://bureau.ru/bb/soviet/20180109/
Удивительно уродские иконки в новом скайпе. Как будто специально старались сделать как можно хуже:

Смотрите, что нашли ребята в чате. У «Шаболовской» латиница поменялась местами с кириллицей, видимо, чтобы кириллица не слиплась с кружком «Октябрьской». Офигенно!

Среда, 10 января
В связи с последними событиями в мире графического дизайна вспомнил две старых заметки про ромбы. Одна:
https://ilyabirman.ru/meanwhile/all/red-squares/
И вторая:
https://ilyabirman.ru/meanwhile/all/rhombus/
Пять лет назад мы в бюро зафигачили дизайн мобильного приложения «Связного банка». До сих пор приятно посмотреть:
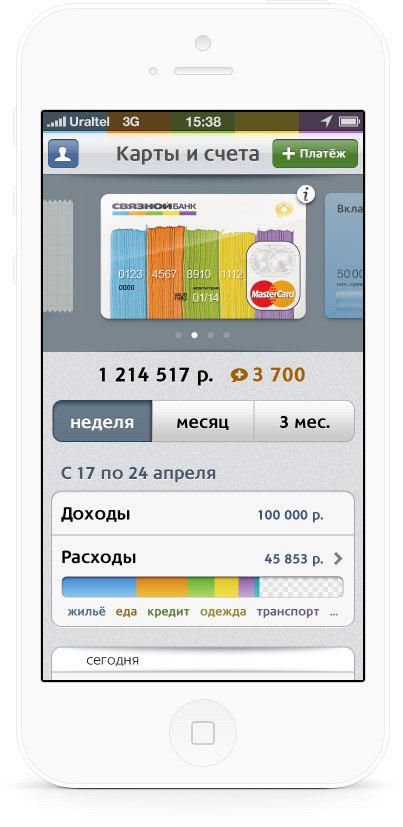
Постепенно все банки слизали наш дизайн с листалкой продуктов сверху и информацией о продукте снизу:
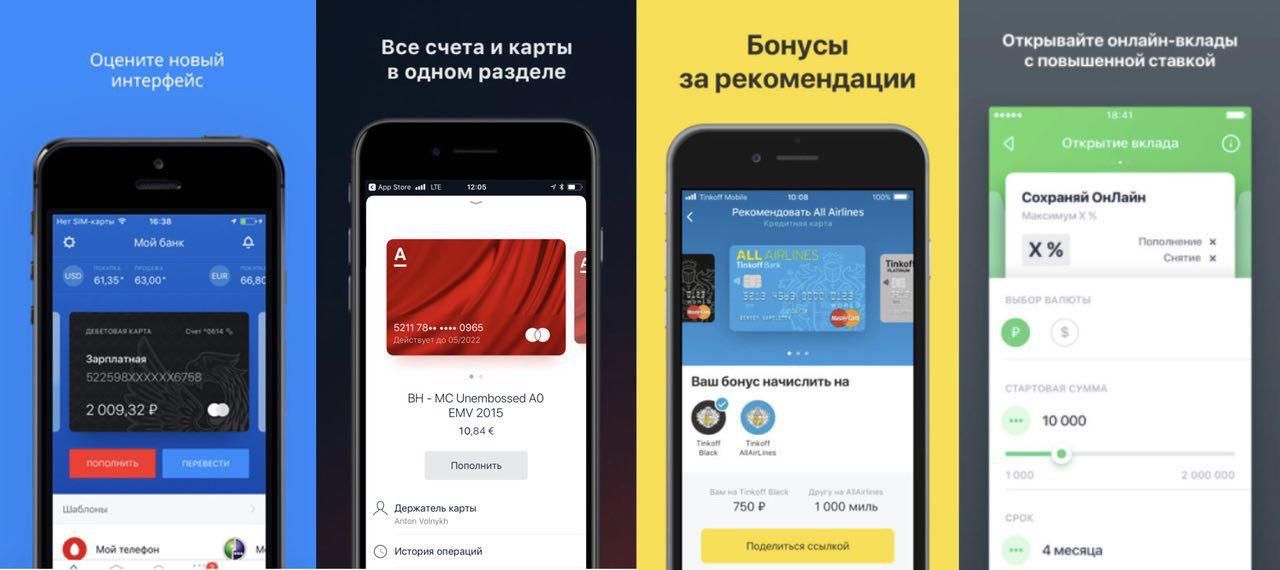
Эту картинку мне принёс Антон Вольных, который руководил проектом со стороны Связного банка тогда.
О проекте на сайте бюро:
https://bureau.ru/projects/svyaznoy-iphone/
Пошёл листать другие проекты для «Связного» и нашёл ещё красоты:
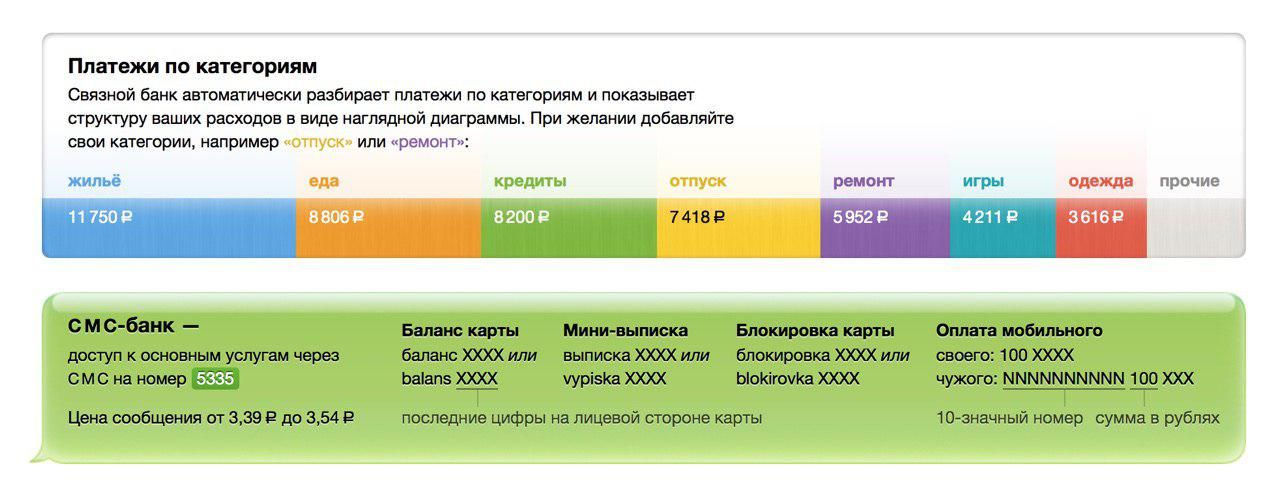
В музеях я стараюсь подходить к картинам, которые привлекли взгляд издалека, а потом пытаться понять, что именно привлекло.

Вот это странное, например. Горизонт завален, в цветах вроде тоже ничего интересного, слева дерево кропнулось непойми как. Но почему-то картина привлекла. Возможно, контрастом (соседние картины более ровные) и формой деревьев. Ещё оказалось, что оттенки чёрного в самом дереве на переднем плане очень богатые, я прям рассматривал их. На фото нифига не видно, потому что в тель-авивском музее искусства очень плохой свет.
Миша Нозик:
Меню:

Зато смотрите, какая крутая иконка «Войти»!
Четверг, 11 января
Как люди воспринимают информацию. Я сегодня проводил воркшоп про дизайн веб-форм в Гугль-кампусе. Один чувак пришёл и был уверен, что будет что-то про Гугль-формы (программа для проведения опросов и тестов).
А ещё там навигация такая:

Допустим, я пришёл в Гугль. На какой мне этаж ехать? Эта штука не помогает понять ничего кроме того, что Гугль отхапал много этажей. Но для навигации эта информация бесполезна.
Илья Пеняев:
Круто, линейные размеры терминала — в минутах ходьбы:
Кто забыл, это офигенный логотип шахматного чемпионата 2018:

Сегодня встретились с Ильёй Мерензоном, главой World Chess. Я спросил, почему логотип получился именно таким. Илья:
Я хотел, чтобы было про двоих людей и провокационно. Шум получился из-за того, что люди подумали, будто мы даже не заметили сексуального подтекста. Хоть этот логотип мы и используем везде, мы сделали ещё безопасную версию, и именно её называем „официальной“. Например, на приглашениях для английской королевской семьи мы поставим „официальный“ логотип, потому что там этот будет не очень уместен. Но этот прекрасно работает на пиар шахмат, мы продаём мерч, у нас уже купили сотни плакатов арт-директора разных крутых фирм, например Адидаса. Нам важно, чтобы у людей было ощущение, что шахматы — это круто и интересно, это привлекает людей, мы получаем больше спонсорских контрактов. Вообще, наше внимание к дизайну очень хорошо окупается.
На вопрос о логотипе «Универсальной логистики» (к которому Илья как раз не имеет никакого отношения), он ответил: «Мне понравилось».
Силами чатика изготовили спецверсию логотипа для арт-директора Адидаса:

Суббота, 13 января

Когда-то я рисовал такую картинку для бюрошного концепта умной парковки:

Вы можете заметить, что внешняя линия здесь жирнее других.
Когда я нарисовал первый вариант, у меня жирным был контур машины, а «выступающие» части — зеркала, верхние крепления, колёса — были тонкими.
А Артём попросил обвести жирным всё по периметру.
Мне эта просьба показалась очень странной: получается, что разные части одного и того же колеса нарисованы разной толщиной. Или вот контур машины вдруг становится тонким в районе зеркала. Нелогично!
Тогда Артём показал мне клёвую ПДФку, объясняющую разное про толщины линий на таких иллюстрациях:
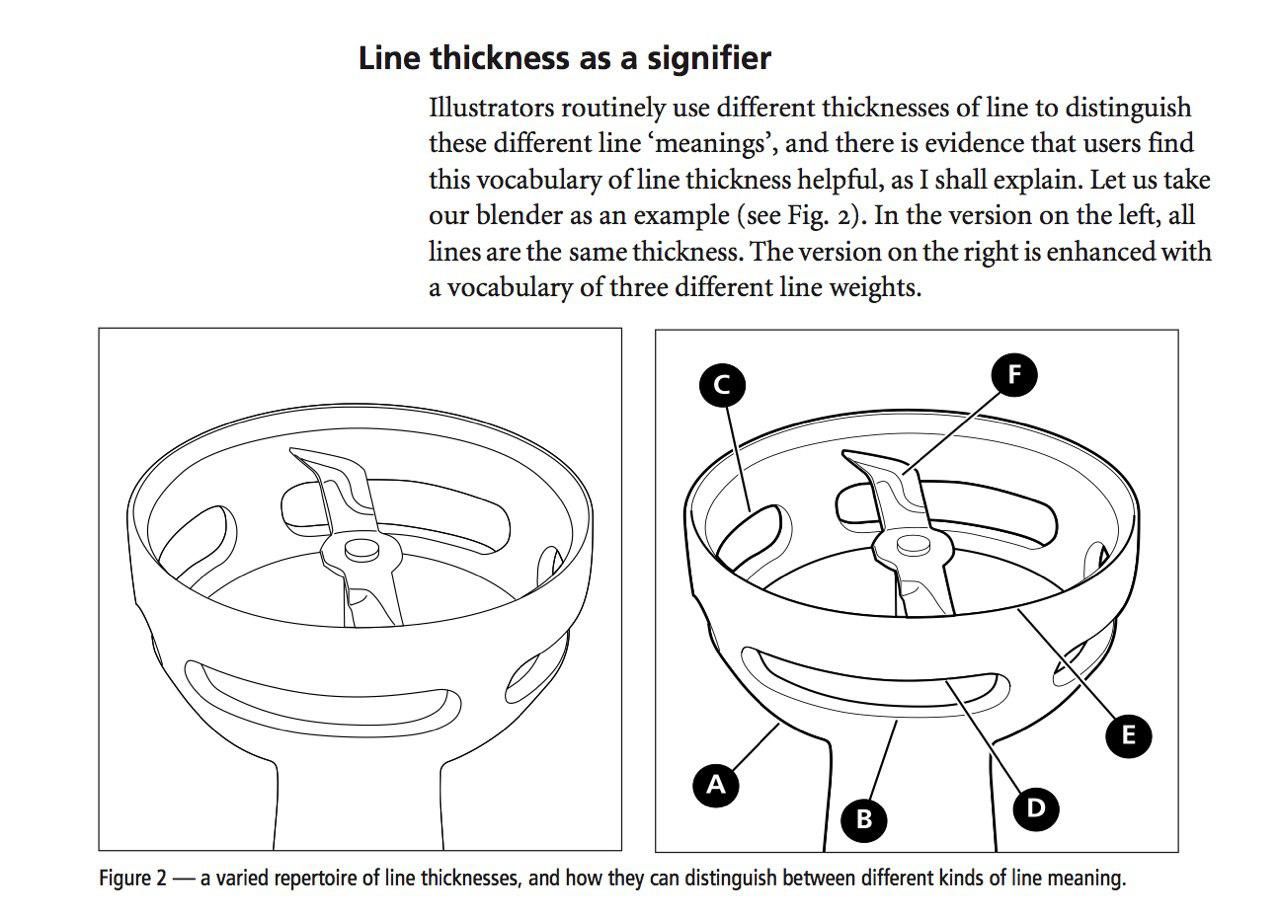
A — это контур, он жирный, тут всё ясно.
B — это встреча двух видимых поверхностей под углом, тонкая линия.
C — снова контур; хоть и внутри объекта, но через него видно фон, поэтому он жирный.
D — дырка другого типа: через неё не видно фон, поэтому тут линия тоньше контурной, но всё же толстая.
E — самая странная линия, потому в ближней к нам части она похожа на D, а в дальней — на B, и возникается неприятный скачок.
F — тонкие линии для передачи формуы и остроты лезвий.
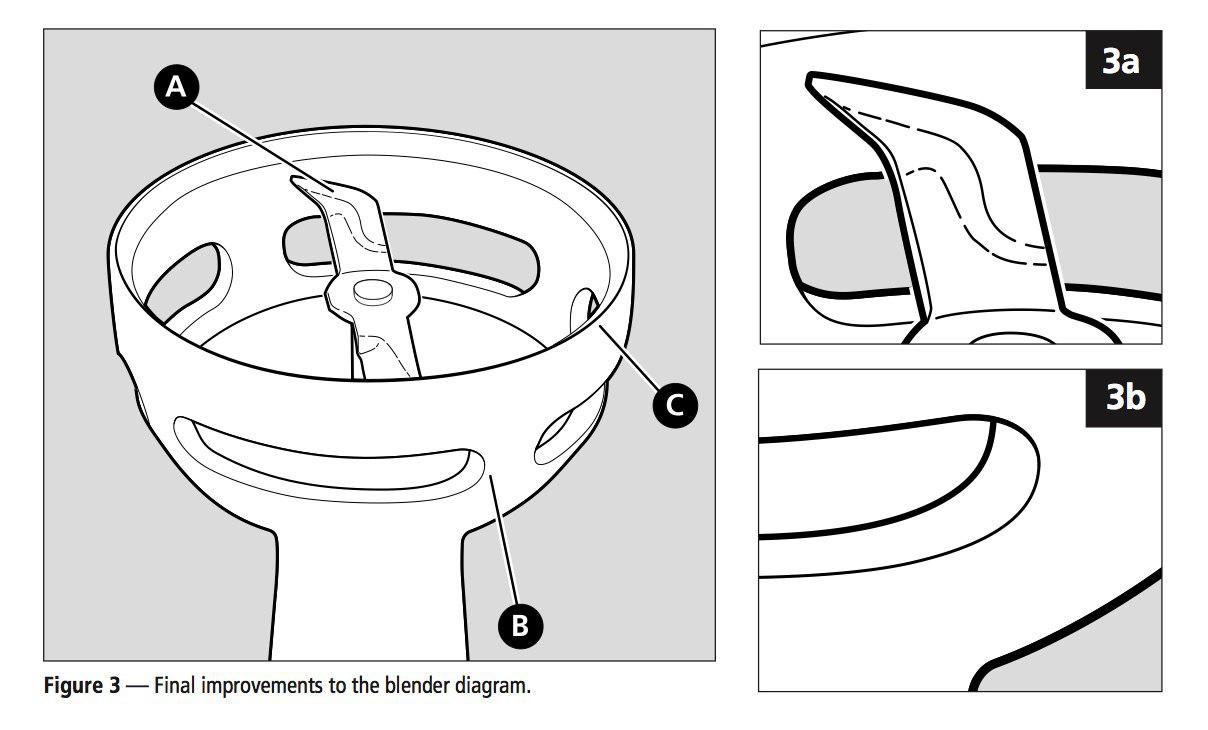
На этой картинке автор победил скачок в толщине линии (тут она уже называется C), сделав её толщину плавно изменяющейся.
Вся эта штука показывает, что соображения для выбора толщины линий вообще связаны не со структурой самого трёхмерного объекта, а с тем, как мы его видим с нашего угла зрения.
Но самое моё любимое тут — это объяснение особого значения контура в иллюстрации; почему он должен быть жирнее всего остального:

Я всегда нахожу этот документ по словам «focal discontinuity», потому что они врезались мне в мозг тогда и всё стало понятно. Ну и звучит красиво.
Проект про парковку (восемь лет назад!):
https://bureau.ru/projects/parking/
Line thickness, a means of expression, by Conrad Taylor:
http://www.conradiator.com/resources/pdf/Linethicknesses.pdf
Дайджест подготовил Иван Ветошкин.



Ромб — это не только квадрат. Побуду немного кэпом и скажу, что ромб — это параллелограмм, у которого все стороны равны. Если точнее, то это — геометрическая фигура, у которой равны все стороны и противолежащие углы. Т. е., по сути-то, квадрат — это тоже параллелограмм, у которого все стороны и углы равны.
Понятное дело, что если квадрат повернуть на 45°, то он останется всё тем же квадратом. Квадрат, получается, он и параллелограмм, и прямоугольник, и ромб в одном лице. В таком случае, лучше дать другое определение: квадрат, повёрнутый ровно на 45°, считается ромбом. Если не на 45, то это уже просто квадрат, потому что если начать крутить ромб, то, с геометрической точки зрения, он всегда останется ромбом, хоть и будет косить под параллелограмм.