Основная теорема анализа

Как-то мы с отцом ехали вдвоём далеко на машине. А это хороший повод для умной беседы.

Речь зашла об «основных теоремах». Основная теорема арифметики — это что любое целое раскладывается на произведение простых чисел, и единственным образом. Основная теорема алгебры — это что у многочлена столько корней, какой он степени (хотя там с формулировками ад). А основная теорема анализа у меня как-то вылетела тогда из головы.

Отец предположил, что основная теорема анализа — это теорема Ньютона—Лейбница. «Это про что?» — спросил я. Отец: «Точную формулировку не помню, но что-то о том, что интегрирование — это операция, обратная дифференцированию».

Стоп, а это разве не по определению?

Как всегда с этими основными теоремами, сказанное в них кажется очевидным после того, как ты уже это прошёл. Но на самом деле именно основная теорема позволяет нам считать интегрирование и дифференцирование обратными операциями. Дальше пойдут глубоко антинаучные рассуждения, где любой математик найдёт 100500 формальных ошибок, но это сейчас не важно.

Что такое дифференцирование? Это когда мы в каждой точке функции проводим касательную и находим тангенс угла, под которым она проходит к горизонту, вот этого:

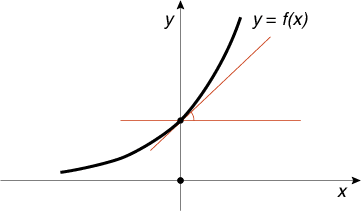
Теперь если каждой точке поставить в соответствие найденный тангенс, то получится новая функция, которая называется производной. Напомню, что число e как раз знаменито тем, что производная функции e^x равна e^x, то есть в каждой точке тангенс угла как раз равен значению самой функции.

Что такое интегрирование? Это нахождение площади фигуры под кривой функции, ограниченной некими вертикальными границами a и b и горизонтальной осью:

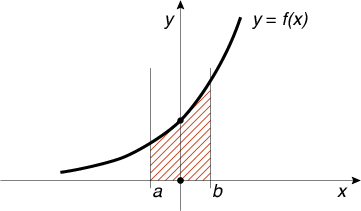
Легче всего считать площадь прямоугольника. Можно разбить кривую, например, на пять прямоугольников и сложить их площадь:

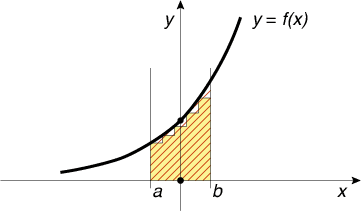
Если делить на всё большее число прямоугольников и посмотреть предел суммы площадей, то получится как раз площадь этой фигуры. Эта площадь называется определённым интегралом функции y = f(x) на отрезке [a; b] и обозначается вот так:

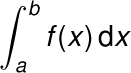
Прямо скажем, совсем не очевидно, что фигня про углы и фигня про площадь вообще как-то связаны.

А связаны они вот как. Обратная производной функция называется первообразной. Первообразная от f(x) — это такая функция g(x), что её производная g´(x) = f(x). Например, у функции y = x² + 8 производная y = 2x. Значит для функции y = x функция y = (x² / 2) + 4 является первообразной.

Легко заметить, что таких функций бесконечное множество. Например, производная функции y = x² + 28 это тоже y = 2x. Значит для функции y = x функция (x² / 2) + 14 тоже является является первообразной. Это логично, ведь производная — это угол в каждой точке, и естественно, что он не меняется от того, на какую высоту мы вертикально поднимаем весь график функции целиком. Значит для функции x первообразная — это x² / 2 плюс сколько угодно.

Так вот, оказывается, чтобы найти площадь фигуры под функцией y = f(x) в пределах от a до b, нужно взять значения любой из её первообразных g(x) в точках b и a и вычесть одно из другого:

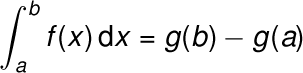
Здесь g — хоть и любая, но всё-таки какая-то одна первообразная, поэтому «сколько угодно» у неё будут одинаковыми, вычтутся друг из друга и на результат не повлияют. Можете взять какую-нибудь простую функцию вроде y = 2x, где площадь и без интегралов легко посчитать в уме, и проверить. Работает!

Эта формула и называется основной теоремой анализа или теоремой Ньютона—Лейбница. Если её доказать, то можно уже называть нахождение первообразной интегрированием и вообще относиться к дифференцированию и интегрированию как к взаимно-обратным операциям.