Доказательство теоремы Пифагора
Так вышло, что когда мы в школе проходили теорему Пифагора (естественно, с доказательством), я болел, поэтому доказательства этой теоремы я никогда не знал, и фраза «Пифагоровы штаны во все стороны равны» мне ни о чём не говорит, хотя я и в курсе, что она каким-то образом связана с рисунком, использующимся в одном из способов доказательства.
У Тафти в Envisioning Information (с. 84) приведено совершенно блестящее доказательство, отходящее от классической математической нотации в сторону внятной информационной графики:
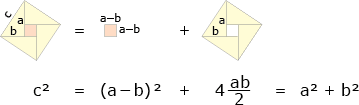
Автору не потребовалось ни называть точки, ни комментировать построения, ни нумеровать формулы и рисунки.
Если кто-то может привести другие примеры красивых доказательств чего бы то ни было, приводите.


Очень много красивых доказательств постит ЖЖ-юзер avva.
К сожалению, вместо того, чтобы ставить рисунки, он абзацами расписывает, как эти рисунки нарисовать. Но зато у него я нашёл ссылку на интереснейшую лекцию Зализняка :-)
http://img214.imageshack.us/img214/5727/sumif8.png
Хорошее доказательство.
А мы в школе доказательство теоремы Пифагора мы не проходили, но когда поступал, попался билет, в котором было задание эту теорему доказать.
Одно из самых красивых — делаем то же самое, только треугольники и квадраты заполнены жидкостью. Переливая из одних в другие, доказываем, что площади равны. Я типа физику люблю, поэтому мне запомнилось вот это.
Это далеко не самое красивое доказательство. Самое красивое здесь:
http://upload.wikimedia.org/wikipedia/commons/e/e8/Pythagorean_proof2.png
Его можно сделать ещё красивее — убрать все символы и треугольник снизу, вместо него написать «Смотри!».
Никаких формул не надо. Кстати, оно есть на стене в одном из кабинетов здания на Володарского, 18.
Ещё пример: древнеиндийская теорема о том, что площадь круга равна равна площади прямоугольника, стороны которого суть полуокружность и полудиаметр круга.
http://www.trinitas.ru/rus/doc/0202/007a/pic/0021/0021-069.gif
А вот ещё — геометрическое доказательство неравенства Юнга:
http://ega-math.narod.ru/Bellman.htm#sect15
Но всё это на школьном уровне. Красивое доказательство не обязано быть геометрическим.
«Здание на Володарского, 18» — отличный эвфемизм :-)
Картинка по второй ссылке мне непонятна. Там круг и прямоугольник разбиты на одинаковое количество фигур, но они не только не равны; те из них, что составляют окружность, даже не являются треугольниками. Кроме того, совершенно неясно, из чего следует равенство длины полуокружности и длинной стороны треугольника; выделения обеих линий жирным ничего не доказывает.
Да, самое красивое это, конечно, «Смотри».
Речь идёт об одном из аналогов метода исчерпывания, в котором количество секторов устремляется к ∞, при этом каждый сектор по форме становится бесконечно близким к треугольнику (площадь «сегментного остатка» имеет больший порядок малости, чем площадь самого треугольника).
Все никак не соображу, а 4ab/2 откуда взялось?
Площадь четырёх прямоугольных треугольников с катетами a, b каждый.
ab — площадь прямоугольника со сторонами ab. ab/2 — площадь треугольника, полученного рассечением этого прямоугольника диагональю.
Извините, но то, что строна оранжевого квадратика равна a—b совсем не очевидно. Т. е. это конечно так, но это надо доказать.
Это не нужно доказывать, ведь ясно, что все 4 треугольника — одинаковые.
Фрагмент оранжевого квадратика даже не равен, а фактически являет собой часть отрезка a без отрезка b.
О... наконец-то понял. Никак не мог найти место где из а можно вычесть b :)
Преподаватель математики как-то дал мне книжку Proofs without Words.
http://www.amazon.com/Proofs-without-Words-Exercises-Classroom/dp/0883857006
Да.. действительно красивое доказательство...
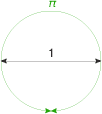
Это не доказательство, а способ вычисления числа Пи. Узнал о нем в книге Нассима Талеба «Одураченные случайностью».
Если вписать круг внутрь квадрата и стрелять в получившуюся картину некоторыми пулями, то следует предположить равные вероятности попадания пуль в любую точку картины (равномерное распределение).
Отношение пуль внутри круга к количеству пуль внутри и вне круга даст значение Пи с бесконечной точностью при увеличении количества пуль.
На это, как я и говорил, — это не доказательство, а метод. На мой взгляд, очень занятный.
http://ru.wikipedia.org/wiki/Метод_Монте-Карло
Возвращаясь к теме 0,(9). Напишите как оно должно быть: число, что отличается от «1» на бесконечно малую величину.
1-0,(0)1=?
Что?
так, из «1» вычитаем «положительный» 0. Получится некая величина. Положительный 0 — бесконечная последовательность (F(x)=1/∞).
Не могли бы вы указать, на какую математическую теорию вы опираетесь?
0,(9) — вещественное число. Ни в теории вещественных чисел, ни в теории пределов, рядов; ни в комплексном, ни в векторном анализе, ни в операционном исчислении я не встречал положений о том, что число 0 может иметь знак. Ни в каких из изучавшихся мною теорий число не может являться последовательностью.
имеется в виду не то, что сам 0 имеет знак. Есть некая функция, которая в пределе стремится к 0 справа или слева. Суть одна. Предел этой функции по сути и является бесконечно малой величиной. Так вот, мне интересно, как записать число, которое отличается от 1 на эту самую бесконечно малую (странно, но в голове только один вариант 0,(9) ). Второе, чем я задаюсь: раз бесконечно малая есть не какое-то конкретное число, а функция, или даже предел функции, то чем будет являтся то число, что отличается от 1 на бесконечно малую.
Предел функции, которая в пределе стремится к нулю (повторяю вашу формулировку) равен нулю. Число, отличающееся от 1 на 0 можно записать разными способами: 1; 0,(9); +1; 1,000 и т. д.
Ок. a/b=0, если а=0, так? Значит, 1/бесконечность не равно 0, т. к. 1 не равен 0. 1-a=1, если a=0. но 1/бесконечность (0,(0)1) не равно 0. Значит, 1-0,(0)1 не равно 1. эта величина отлична от 1 на бесконечно малую. как ее записать? возможно, что так будет понятнее о чем я пишу. Самое простое и очевидное на первый взгляд, что эта величина и есть 0,(9). Поправьте, если я не прав.
«a/b=0, если a=0» — такого постулата нет, но когда b не равно нулю это следует из определения деления. «Значит» — логический переход неверен («если все голуби — птицы, значит все неголуби — не птицы»). «1/бесконечность» — бесконечность не является числом, делить на неё нельзя. «0,(0)1» — запись ничего не означает, такой записи не существует.
Вы не правы в том, что берётесь рассуждать о числах, не имея о них понятия, с полной кашей в голове: бесконечность, число, величина, функция, последовательность, предел — вам безразлично, что означают эти слова, вы спокойно делите их друг на друга, утверждаете их равенство или неравенство, делаете какие-то выводы из результатов.
Вы упрямо уходите от ответа. Итак понятно, что на ноль делить нельзя. бесконечность — некое абстрактное понятие, т. к. числовая прямая не имеет конкретного предела. но суть не в споре о понятиях. вопрос стоял следующий: как записать выражение вида 1-бесконечно малая величина? бесконечно малая величина — величина пусть и абстрактная, но которая совершенно точно не равна 0.
Вы говорите: «я придумал абстрактное понятие, не важно что оно значит, но меня волнует, что будет, если его вычесть из единицы». Этот вопрос не имеет вообще никакого смысла. Вы хотите, чтобы я понял, что вы имеете в виду, тогда как вы даже сами не можете этого понять. Я указываю вам на огрехи в ваших рассуждениях в надежде, что это поможет вам сформулировать ваши мысли более внятно, а вы это воспринимаете как уход от ответа.
Бесконечно малая величина — это число? Раз вы сравниваете её с нулём, значит да. Раз это число, не равное нулю, пусть это будет число 47. Тогда 1-47 = -46. Очевидно, это не тот ответ, который вы ждёте. Следовательно, помимо неравенства нулю, у вашего мифического числа есть ещё какие-то свойства. Не могли бы вы их сформулировать? Возможно, это приблизит нас к ответу.
Кстати на счет деления на ноль и много чего еще :-) есть отличная статья http://www.proza.ru/texts/2008/08/02/228.html
Все объясняется на вениках. Рекомендую к прочтению.
MjStalker, фигня это полная, а не статья. Автор бредит. А уж когда начинает разговор про рождение Вселенной — то это уже клинический случай.
Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов. Поэтому нам ничего не остается, как рассмотреть некоторые классические доказательства теоремы Пифагора, известные из древних трактатов. Сделать это полезно еще и потому, что в современных школьных учебниках дается алгебраическое доказательство теоремы. При этом бесследно исчезает первозданная геометрическая аура теоремы, теряется та нить Ариадны, которая вела древних мудрецов к истине, а путь этот почти всегда оказывался кратчайшим и всегда красивым».
Теорема Пифагора гласит: «Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах». Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы.
Во II веке до нашей эры в Китае была изобретена бумага и одновременно начинается создание древних книг. Так возникла «Математика в девяти книгах» — главное из сохранившихся математико-астрономических сочинений. В IX книге «Математики» помещен чертеж, доказывающий теорему Пифагора. Ключ к этому доказательству подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами и гипотенузой С уложены так, что их внешний контур образует квадрат со стороной А+В, а внутренний — квадрат со стороной С, построенный на гипотенузе. Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника, то ясно, что образовавшаяся пустота, с одной стороны, равна С в квадрате, а с другой — А+В, т. е. С=D+B. Теорема доказана.
Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII века в Бхаскары помещен чертеж с характерным для индийских доказательств словом «смотри!». Прямоугольные треугольники уложены здесь гипотенузой наружу и квадрат С перекладывается в «кресло невесты» квадрат А плюс квадрат В. Частные случаи теоремы Пифагора встречаются в древнеиндийском трактате «Сульва сутра» (VII-V веках до нашей эры).
Доказательство Евклида приведено в предложении 1 книги «Начал». Здесь для доказательства на гипотенузе и катетах прямоугольного треугольника строятся соответствующие квадраты.
«Багдадский математик и астроном Х века ан-Найризий (латинизированное имя — Аннариций), — пишет Волошинов, — в арабском комментарии к «Началам» Евклида дал следующее доказательство теоремы Пифагора. Квадрат на гипотенузе разбит у Аннариция на пять частей, из которых составляются квадраты на катетах. Конечно, равенство всех соответствующих частей требует доказательства, но мы его за очевидностью оставляем читателю. Любопытно, что доказательство Аннариция является простейшим среди огромного числа доказательств теоремы Пифагора методом разбиения: в нем фигурирует всего 5 частей (или 7 треугольников). Это наименьшее число возможных разбиений».
Посмотрев на вашу запись подумал о доказательстве формулы (a-b)^2
Может не очень красиво, но вот нашёл примеры доказательств этой и подобных формул.
Точно помню что в школе похожие доказательства висели на стенах, но нам доказывали алгебраическими методами.
http://www.metodika.ru/?id=76
Так тут нужно просто скобки раскрыть.