Параллельные реки
Представим себе, что две реки текут как-то более-менее параллельно.
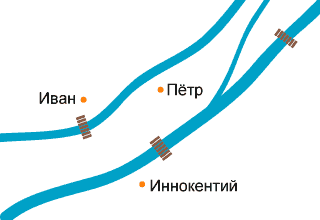
Иван, Пётр и Иннокентий живут в домах, обозначенных на рисунке оранжевыми точками. На реках периодически встречаются мосты, которые обозначены коричневой фигнёй.
Вопросы:
- Могут ли Иван и Пётр ходить друг к другу в гости?
- Могут ли Пётр и Иннокентий ходить друг к другу в гости?
- Могут ли Иван и Иннокентий ходить друг к другу в гости?
Ответы могут вам показаться очевидными — это не беда; всё равно, дайте их пожалуйста. Постарайтесь при этом воздержаться от предположений о том, зачем я это спрашиваю.
Update: Не нужно умничать или пытаться быть невероятно оригинальным. Если не хотите отвечать на вопрос, лучше не отвечайте вообще. Если шутите, шутите смешно.




Даю очевидный ответ:
У меня несколько версий.
1) Не могут.
Цветовое кодирование данной схемы говорит нам, что Иван, Пётр и Иннокентий — одно лицо.
2) Могут.
Поскольку размер оранжевой точки значительно больше промежутков между коричневыми палочками моста, они не будут проваливаться в реку.
3) Х.З.
На схеме мы видим лишь обозначения местоположения Ивана, Петра и Иннокентия, но абосолютно не очевидно, где у них дома.
да
да
и да
да, да, да
Да, да, да.
Наверное они могут ходить друг к другу в гости независимо от наличия всяких рек и мостов.
А зачем лишняя коричневая фигня?
Просто так.
В любом случае, они могут построить новый мост или заказать резиновую лодку в интернет-магазине. Главное желание.
Да, да, да.
Нет, это изменит условие задачи. Мосты есть только там, где есть. Интернет-магазина нет.
Любой случай не интересует, интересует этот.
Драма: «Иван, Пётр, Иннокентий и горбатая река».
В четырёх томах.
Эта книга о трагических взаимоотношениях трёх молодых ковбоев, живущих в оранжевых домах на берегах реки Уй в Уйской области Семёновского уезда. Отсутствие современных коммуникаций в виде международной сети Интернет и перманентное неудобное расположение подозрительно коричневых мостов на реке Уй не давало развиваться их чувствам…
Да, да, да.
Я даже могу нарисовать маршруты, по кототрым они будут ходить в гости друг к другу :)
Итак ответ: смогут, если на пути этих маршрутов не встретятся какие-либо другие непреодолимые преграды.
И причем здесь характеры героев, если вопрос о теоретических возможностях?
Спасибо.
Я убрал комментарии про характеры героев :-)
Абсолютно ни при чём. Тем более, что они явно скверные.
Я считаю, что теоретическая возможность ходить в гости, при сегодняшнем активном развитии гражданской авиации, у них была бы и при полном отстутствии мостов.
Да, да, да. Математики бездушные :-)
Одновременно — не смогут.
А на заданные вопросы, сделайте одолжение, ответьте?
Как вы объясняете то, что ваши ответы расходятся с ответами всех остальных?
Если не добавлять неочевидных условий (например, что все перечисленные товарищи — безногие, или что у них нет домов, в которые можно прийти в гости) и сделать очевидные предположения (что синими линиями обозначены реки, коричневыми чёрточками обозначены мосты, а белый фон представляет собой пространство, доступное для передвижения пешехода), то на все три вопроса ответ «да».
Где-то здесь н**бка, конечно, но всё-таки: да, да, да.
Здесь всё чисто, правда.
Илья, а почему вы снесли систему тегирования на вашем блоге как раз тогда, когда мне она понадобилась? И, собственно, для чего?
Это временно и по техническим причинам.
Трижды да.
Потому, что они должны быть друг с другом знакомы.
Дак они друг с другом знакомы.
Вызывает сомнение существование таких двух примерно параллельных рек, когда расстояние между ними в 3 раза больше длины моста :)
Условие задачи не может вызывать сомнений. Это называется «Дано». Это аксиома.
Имеется в виду, существование в реальности.
Что касается ответов на поставленные вопросы, из сказанного не видно, почему они не могли бы ходить в гости друг к другу. Да, да, да.
Три раза «да».
Да^^3
С точки зрения «обычного» человека — да, могут.
С точки зрения математической задачки (если рассматривать её так) задачка некорректная. Не понятно, что значит «ходить в гости». Как, например, переложить эту задачку на графы? Там всё вполне формально можно было бы описать. И там же появляются вопросы всякие...
Задача не математическая, а сугубо жизненная.
В жизни обычно вопросы ставятся не так, а несколько иначе: «что мне стоит пойти в гости туда и что я от этого получу?» А не «могу ли я пойти». Нет ничего невозможного для человека с интеллектом.
Так что могут. В любом составе и к кому угодно в гости.
Естественно, интересен не ответ, а кто как считает.
http://ilyabirman.ru/meanwhile/2003/05/02/1/
да, да, да
да, да, да и живут они в одной плоскости.
1,2,3) Могут, но не обязательно будут из чисто человеческих побуждений.
Могут.
А ещё мы можем в субботу пойти в гости к, например, Аткину.
Вот, собственно, в том то и дело.
Скорее всего, все будут ходить в гости к Петру, потому что он ближе и «по пути», и два моста переходить не надо. :)
А ответ на вопросы даю: да, да, да. У всех есть возможность ходить друг к другу в гости.
1.Нет
2.Нет
3.Нет
Начнем с того, что одновременно Иван и Петр не могут быть у друг друга в гостях.
Так и с остальными. И опять же если Иван в гостях у Петра, то один из них не в гостях по умолчанию.
Картинка только отвлекает.
Да, конечно. (На все три)
2 exdeniz: ответ оригинальный, но обоснование хромает. «Друг к другу» не подразумевает синхронность действий.
Илья, ты собирал статистику понимания этого выражения?
Да, да, да.
Да, да, да.
Ответы:
Да * 3.
Да, да, да.
Видимо, это тест на то, сколько человек видят в текстах Ильи каки-либо на**ки. Я не вижу.
Да. Да. Да. Если под походом в гости понимается обычное, жизненное, а вовсе не вырожденные случаи, как то предполагал exdeniz.
Да, да, да.
Ответы: да; да; да. В Снккт-Петербурге, к примеру, такое сплошь и рядом: http://maps.yandex.ru/map.xml?mapID=3&size=1&scale=5&mapX=6348880&mapY=6648920&act=5&mapWidth=4000
Иван, Иннокентий и Пётр могут все. это вопрос мотивации и веры в свои возможности
Да, да, да.
это ж очевидно 1)Да 2)Да 3)Да
Да, да, да — а объяснение будет? :)
Зачем же? ;-) Я выяснил то, что меня интересовало.
!!Я выяснил то, что меня интересовало.!!
А что вас интересовало, если не секрет? Количество читателей, их активность, процент девиаций?
Я же написал где-то там выше — меня это интересовало в связи с вообще другой задачей со сходными условиями. Это вообще никак не связано ни с читателями, ни с активностью, ни с девиациями. Возможно, через какое-то время станет понятно.
Илья Бирман — rocket scientist =)